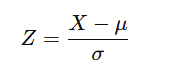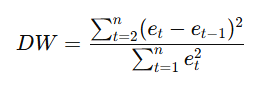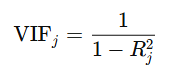Halo, Statistician!
Dalam dunia statistik, memahami bentuk distribusi data adalah langkah awal yang sangat penting. Banyak metode analisis, seperti regresi maupun uji hipotesis mensyaratkan distribusi tertentu seperti normal, binomial, atau lainnya untuk menghasilkan interpretasi yang valid dan akurat. Oleh karena itu, penting bagi kita untuk mengidentifikasi terlebih dahulu bagaimana pola penyebaran data sebelum melangkah lebih jauh dalam analisis.
Kalian tentu sudah tidak asing lagi dengan analisis regresi, salah satu teknik statistik yang banyak digunakan untuk memahami hubungan antar variabel. Namun, tahukah kalian bahwa sebelum menjalankan regresi, ada sejumlah asumsi klasik yang wajib dipenuhi? Jika asumsi-asumsi ini dilanggar, maka hasil regresi bisa menjadi tidak valid, kurang akurat, atau menghasilkan interpretasi yang keliru. Nah, pada pembahasan kali ini, kita akan mengulas tuntas apa saja uji asumsi klasik yang harus dilakukan sebelum kalian menjalankan analisis regresi, baik itu regresi linier sederhana maupun berganda. Berikut ini penjelasan lengkap mengenai uji asumsi klasik yang umum dilakukan:
- Uji Normalitas
Normalitas residual penting agar proses estimasi koefisien regresi dan uji statistik seperti t dan F bersifat valid. Uji ini bertujuan untuk memastikan bahwa selisih antara nilai prediksi dan nilai aktual (residual) menyebar normal.
Metode:
- Histogram residual.
- P-P Plot atau Q-Q Plot.
- Uji Kolmogorov–Smirnov / Shapiro–Wilk.
Rumus Z-score (jika digunakan):
Keterangan:
- X: nilai data.
- µ: rata-rata populasi.
- σ: standar deviasi populasi.
- Z-score digunakan untuk mengubah data menjadi distribusi standar normal.
- Uji Heteroskedastisitas
Heteroskedastisitas terjadi jika residual memiliki varians yang tidak sama di seluruh pengamatan. Ini dapat mengganggu efisiensi estimasi koefisien regresi.
Metode:
- Uji Glejser.
- Uji Park.
- Uji White.
- Scatterplot residual vs nilai prediksi.
Rumus (Glejser):
Keterangan:
- |ei|: nilai absolut dari pengamatan ke-i.
- α: konstanta.
- β: koefisien regresi.
- Xi: variabel independen.
- ε: error.
- Jika nilai signifikansi β\betaβ < 0,05 → indikasi heteroskedastisitas.
- Uji Autokorelasi
Autokorelasi biasanya terjadi pada data runtun waktu (time series), ketika residual satu observasi berkorelasi dengan residual sebelumnya. Ini melanggar asumsi independensi error.
Metode:
- Uji Durbin-Watson (DW).
Rumus:
Keterangan:
- et: residual pada waktu ke-t.
- et-1: residual pada waktu sebelumnya.
📌 Kriteria:
- DW ≈ 2 → Tidak ada autokorelasi.
- DW < 1,5 → Ada autokorelasi positif.
- DW > 2,5 → Ada autokorelasi negatif.
- Uji Multikolinearitas (Khusus Regresi Berganda)
Multikolinearitas terjadi jika terdapat korelasi tinggi antar variabel independen dalam regresi berganda, sehingga menyulitkan interpretasi dan memperlemah kestabilan model.
Metode:
- Nilai VIF (Variance Inflation Factor).
- Nilai Toleransi.
Rumus:
Keterangan:
- Rj^2: koefisien determinasi dari regresi variabel terhadap variabel independen lainnya.
- Jika VIF > 10 menunjukan adanya multikolinearitas yang tinggi.
Untuk memudahkan proses analisis, uji asumsi klasik biasanya dapat dilakukan menggunakan berbagai software statistik seperti SPSS, R, Minitab, maupun Microsoft Excel (dengan beberapa keterbatasan). Penggunaan software ini membantu dalam mempercepat perhitungan, menampilkan grafik pendukung, serta menyajikan output yang mudah diinterpretasikan oleh peneliti atau analis data. Dengan melakukan uji asumsi klasik, kita memastikan bahwa model regresi yang dibangun memiliki dasar statistik yang kuat dan dapat menghasilkan estimasi yang valid dan tidak bias. Untuk regresi linier sederhana, asumsi yang diuji biasanya adalah normalitas, heteroskedastisitas, dan autokorelasi. Sementara pada regresi berganda, pengujian multikolinearitas juga menjadi hal yang sangat penting.
Sumber :
- Hajarisman, N., & Herlina, M. Modul Praktikum Analisis Regresi